Understanding the Difference between Distance and Displacement: Key Concepts and Definitions
Introduction
In this article, let us learn the Difference between Distance and Displacement with key concepts and definitions. The concepts of distance and displacement are fundamental to physics and related fields. While they may appear to be similar, they have distinct meanings and implications. This comprehensive article aims to provide a detailed explanation of distance and displacement, their differences, formulas, and practical applications. It also explores related terms such as scalar and vector quantities, as well as the significance of these concepts in different contexts.
1. Fundamental Definitions:
To lay the groundwork, let's begin by providing fundamental definitions of key terms related to distance and displacement.
a. Distance:
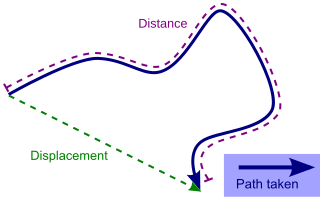
Distance is a scalar quantity that measures the length traveled along a path by an object, without considering its direction or any changes in motion. It is the total length covered and is always positive or zero.
b. Displacement:
Displacement, on the other hand, is a vector quantity that refers to the change in an object's position with respect to its starting point. It considers both the object's starting point and its ending point, as well as the direction it has moved. Displacement can be positive, negative, or zero, depending on the direction of the movement.
c. Path:
Path refers to the route or trajectory an object follows while moving. In the context of distance, it is the actual route traveled and can involve changes in direction. In the context of displacement, the path does not matter; only the initial and final positions matter.
2. Distance vs. Displacement:
Now that we have established the basic definitions, let's analyze the differences between distance and displacement.
a. Conceptual Differences:
Distance is a scalar quantity that reflects the overall length covered during motion, regardless of the starting and ending positions or the direction of movement. In contrast, displacement is a vector quantity that captures the change in position relative to the starting point, taking into account both the magnitude and direction.
b. Significance of Direction:
Distance does not account for direction, as it measures only the magnitude of the total path length traveled. Displacement, however, considers the direction of the movement and is crucial in understanding an object's final position relative to its starting point.
c. Positive and Negative Values:
Distance is always positive or zero since it represents the magnitude of the distance traveled. Displacement can be positive, negative, or zero. It becomes positive when the object moves in one direction, negative when it moves in the opposite direction, and zero when there is no change in position.
d. Examples:
To illustrate the difference, imagine a person walking around a park in a 500-meter loop. If they return to their starting point, the distance traveled is 500 meters (positive), while the displacement is zero (no change in position). However, if the person decides to continue walking in one direction for an additional 500 meters, the distance traveled remains 1000 meters, but the displacement becomes 500 meters (positive direction).
3. Scalar and Vector Quantities:
Understanding the nature of distance and displacement can be aided by differentiating scalar and vector quantities.
a. Scalar Quantities:
Scalar quantities are those that possess only magnitude and units, without any associated direction. Distance, mass, temperature, and time are all examples of scalar quantities. Scalar quantities are manipulated using basic arithmetic operations, such as addition and subtraction.
b. Vector Quantities:
Vector quantities possess both magnitude and direction. Displacement, velocity, acceleration, and force are examples of vector quantities. To describe vector quantities, we use both magnitude (often represented by a number value) and direction (represented by an arrow or compass direction). Vector quantities follow specific rules of vector addition and subtraction, incorporating both magnitude and direction.
c. Relationship to Distance and Displacement:
Distance is a scalar quantity as it only measures the magnitude of motion. Conversely, displacement is a vector quantity because it captures the change in position's magnitude and direction. Therefore, when analyzing motion, it is essential to distinguish between scalar and vector quantities to ensure accurate calculations and understand the complete picture.
4. Distance and Displacement Formulas:
Formulas play a key role in calculating distance and displacement accurately. Here, we present the essential formulas associated with each concept:
a. Distance Formula:
The formula to calculate the distance traveled is derived from the properties of straight lines or curves. Depending on the type of motion, different formulas can be employed. Some common formulas include:
i. Distance Traveled at Uniform Velocity:
Distance = Speed × Time
Where "Speed" is the magnitude of the constant velocity and "Time" is the duration of the movement.
ii. Distance Traveled with Constant Acceleration (Starting from Rest):
Distance = (1/2) × Acceleration × Time^2
Where "Acceleration" represents the change in velocity per unit time, and "Time" is the duration of movement.
b. Displacement Formula:
The formula for displacement considers both the magnitude and direction of the change in position. It can be calculated using the following formula:
Displacement = Final Position Initial Position
Here, the final position refers to the ending point, and the initial position refers to the starting point.
5. Practical Applications:
Distance and displacement concepts find applications in various fields, including physics, engineering, navigation, and transportation. Here are some practical applications:
a. Navigation and GPS:
In navigation systems and GPS devices, understanding distance and displacement is crucial for calculating routes, distances, and times. By considering both distance and displacement accurately, these systems can guide travelers efficiently with precise directions.
b. Kinematics and Dynamics:
In physics, distance, and displacement concepts play a crucial role in analyzing motion. Kinematics, the branch of physics concerned with the study of motion, relies heavily on these concepts to describe and predict motion accurately. Additionally, dynamics, the study of forces and their effects on motion utilize distance and displacement to understand acceleration, velocity, and force interactions.
c. Sports Analysis:
In sports analysis, distance, and displacement measurements aid in tracking athletes' performance, assessing team strategies, and comparing sportspersons' abilities. From analyzing the distance covered during a soccer match to measuring the displacement of a long jumper, these concepts provide valuable insights.
d. Urban Planning and Traffic Management:
Distance and displacement calculations are crucial in urban planning and traffic management to optimize transportation systems. By understanding the distance covered by vehicles and the displacement from starting to ending locations, traffic flow can be optimized, reducing congestion and enhancing overall efficiency.
6. Conclusion:
In conclusion, distance and displacement are vital concepts for the understanding of motion in the fields of physics, engineering, and beyond. While distance and displacement share similarities in the measurement of length, they differ significantly in terms of direction, sign, and conceptual meaning. By distinguishing between scalar and vector quantities, we can quantify distance and displacement accurately, incorporating both magnitude and direction. The formulas associated with these concepts provide a foundation for calculating distance and displacement under various conditions. Additionally, distance and displacement find practical applications in navigation, physics, sports analysis, and traffic management, among others. By grasping these fundamental concepts, one can gain deeper insights into the dynamics of motion and apply them effectively in real-world scenarios.